Miura Folding is a design originally proposed to fold maps by Koryo Miura (Emeritus Professor of University of Tokyo, Former Director of the Institute of Space and Astronautical Science in Tokyo). The design was initially founded upon the question of "What would happen if you fold a single sheet of paper in two directions at once?".
For example, if a single paper is crumpled, a three dimensional ball is formed. While this is true, Miura thought of what would happen if the crumpling took an ordered form. For example, when crushing a metal can, the metal plate folds both in and out of the plane surface of the cylinder, forming a pattern composed of uniform diamond shapes.
When spreading the diamond-patterned surface out flat, a sheet showing regular folding lines is obtained. These folding lines show us the best folding pattern for the sheet.

Miura thought of using this diamond-array structure called the Yoshimura Pattern, and applying it to fold the solar panels of artificial satellites, as well as easily folded maps. This is the origin of Miura Folding. Upon research, Miura discovered the optimal folding angle for these structures to be 6 degrees from a right angle, and since all the folds are independent, the structure can be opened and folded in one motion by simply pulling and pushing on the corners of opposite ends. In order to heighten the degree of recognition of this deployable structure, Miura designed a foldable map.This ground-breaking map folding design was first presented by the name of "Deployable Double Corrugation Surface", but went under-recognized. However, Miura's map created a commotion when introduced at the 10th Conference of International Cartographers in 1980. Afterwards, British Origami Society gave this folding design a more familiarized name of "Miura Folding", which remains to this day.

The best way to understand Miura Folding is to demonstrate it yourself.
It can be done fairly easily using only a single sheet of paper.
Here we will introduce how to perform Miura Folding step-by step. (())

1. Take a sheet of paper and mark it into 5 equal lengthwise strips. (A3 paper is recommended. The larger the paper the easier to fold.)


2. Fold along the lines alternately between mountain folding and valley folding (like an accordion) until it is a single narrow strip.


3. Fold the end of the strip in the ratio 4:3 but make sure so it is skewed. (The angle should be about 6 degrees from a right angle.)


4. Fold the end back again so it is parallel to the original strip, making a skewed square


5. Fold the short end into three equal cells, and the long end into four. This will make a total of 7 horizontally folded cells.


6. You will now have a single folded structure where the overlapping cells are slightly skewed.


7. Now spread out the paper and lay it flat. Seven zigzagging lines run across the sheet. Using these as guides, once again alternate mountain and valley folds.


8. Push the zigzagging mountain folds together to compress the structure. This may take some repeated trials, but eventually the structure should collapse upon itself.


9. Try opening the sheet once more and check the design. An array of parallelograms should be seen. By pulling on the diagonal corners, the structure can be opened and closed in a single motion.

With this, Miura Folding is complete!

1. Miura Folding in nature
One may not notice, but upon taking a closer look at our surroundings, Miura Folding and its related designs can be found around us in a vast array of structures.

Although Miura Folding was invented in relatively recent years, nature has found a way of devising structures with similar folding designs from long ago. A prominent example is the leaf bud of the European hornbeam. Before budding, the hornbeam leaf is tightly is packed and folded in, but upon budding, the leaf expands to make a broad planar structure.
Compared to the leaf in its fully grown state, the leaf bud is evidently much smaller in width and length. Of course, the leaf will continue to grow after budding, but the just-budded leaf is nonetheless professedly greater in size when compared its contracted state before budding. The expansion mechanism of the leaf can be easily understood by practicing the Origami design called "Ha-ori", or "leaf-folding" in Japanese (Kobayashi, Kresling, & Vincent, 1998).

Fig.1 The Ha-Ori leaf-folding

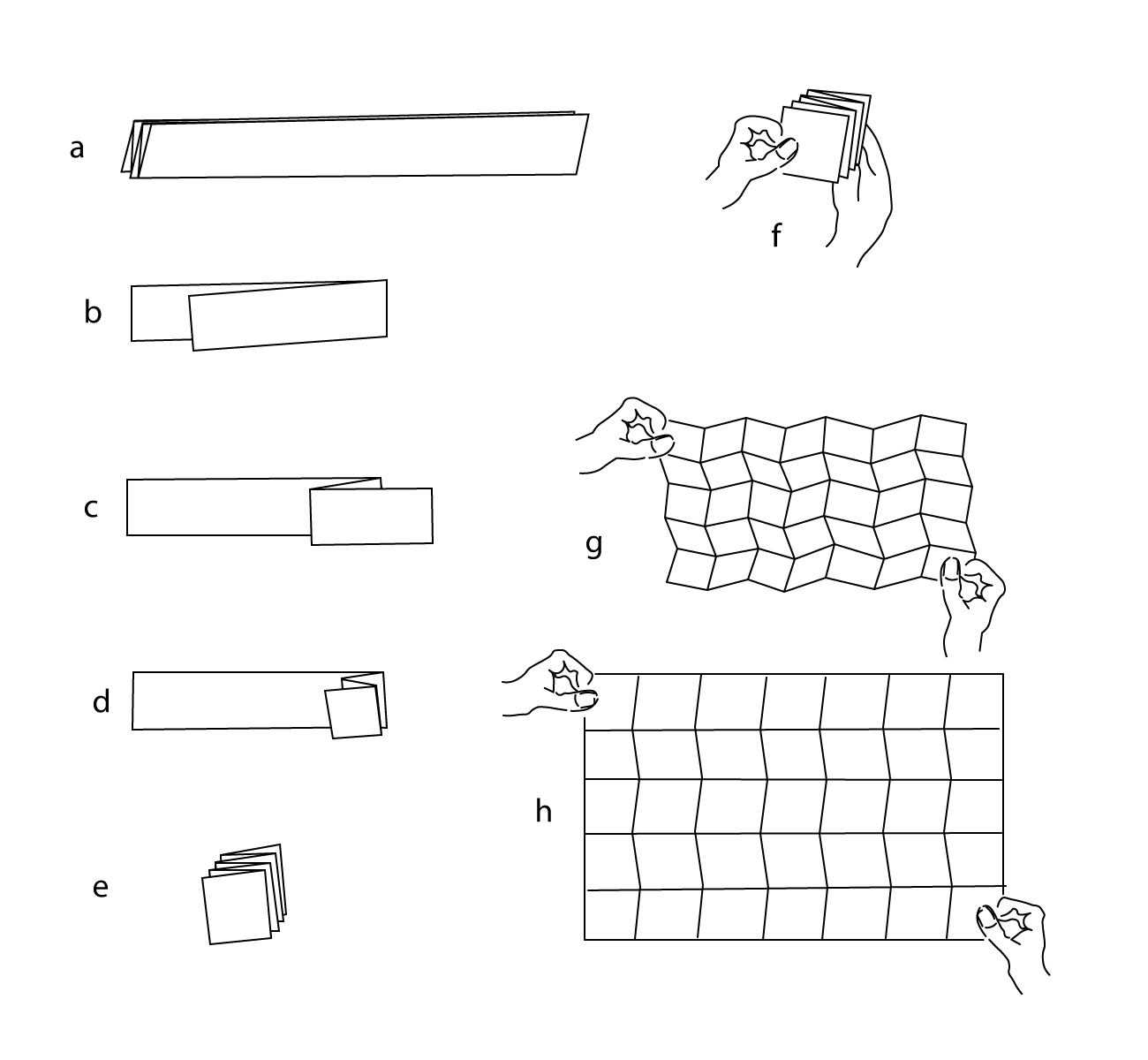
Fig.2 How to make a Miura-ori map

The Ha-ori design was first proposed by German designer Biruta Kresling. Kresling was inspired by the pleated design of hornbeam tree leaves and modeled their appearance with Miura-like folds. As seen in the figure, the design consists of ridges and valleys making pleated folds which are aligned in a flying V-shape.
The folds are interconnected, allowing whole structures to be folded and unfolded from a single or multiple driving points. By pinching on the ends, the structure can be folded into a flat, folded strip, and while pulling on the ends will open the leaf, revealing a broad planar structure. Ha-ori leaf folding is now often introduced as an education tool to better understand the structures of tree leaves in nature.

Other Miura-folding like structures in nature may the include the designs of insect wings, such as in the zig-zagged wing bases of dragonflies and butterflies. This is thought to enable their wings to neatly fold and expand, and perhaps even help smooth metamorphoses into its adult stages.

2. Space Development
Space satellites require solar panels with large surface area to maximize the energy produced from sun rays.Thus, large solar panels are folded down as much as possible to be packed into the rocket, and are quickly unfolded once in outer space. When the rocket returns to the surface of Earth, they must be once again be folded down and re-stowed.
However, conventional solar arrays have a limitation in size due to volume constraints in rocket payload. In order to solve this problem, Miura Folding was applied to the design of these solar arrays. In 1995, Japan Aerospace Exploration Agency (JAXA) launched the Space Flyer Unit, which was the first satellite utilizing Miura Folding in its solar panels.
Due to its complex folding design, Miura Folding enables the solar panels to be compactly stowed in the rocket and obtain maximum cargo space. Like the leaf design, the solar panels are expanded in two dimensions which also greatly increases the surface area, enabling efficient uptake of sunlight. In addition, since Miura Folding allows folded material to be expanded or contracted in one motion by pulling or pushing its opposite ends, when applied to solar arrays, it can reduce the numbers of motors required to unfold the panels.This reduces the weight and complexity of the structure and provides a highly efficient design with low energy consumption rates. Application of Miura-folding to solar panels greatly influenced the aerospace industry and drew attention to other possible applications of origami engineering, such as in designs of space equipments, robotics, or solar-sail units for long distance space travel.

3. In our daily lives
Another artificial structure derived from Miura Folding would be the Japanese beverage cans made by the Toyo-Seikan Company. These cans use a pre-folded pattern known as Pseudo-Cylindrical Concave Polyhedral (PCCP). Designed by the inventor of Miura folding himself, the cylindrical structures are made up of multiple diamond patterns, giving the can higher resistance to buckling. For pressurized cans, the cans will collapse into pre-folded PCCP patterns the moment they are opened . This design is used for carbonated drinks like sodas and beers as well as coffee. Cans can also come vacuum-packed as in tea drinks, and for these, by being pre-collapsed, the cans can have higher resistance to pressure and prevent collapsing. Both of these designs are efficient manufacturing methods allowing 30% less material usage. Further applications of this design as undersea pressure hulls have also been looked into in recent years.

A variety of other man-made objects employing Miura-like folding exist, such as cornices of Chinese lanterns, surgical devices such as stents, and so on. flexible lithium ion batteries , and so forth. All of these structures have extended the knowledge of origami engineering to realize deployable structures which efficiently transition from one form to another. In our project, we too drew attention to the properties of Miura Folding, and sought to adopt its design to realize transfoldable DNA nanostructures, and furthermore obtain arbitrary forms.

Go back to Design